Getting Started
Welcome to the exhilarating world of GPU computing, where raw computational power meets limitless possibilities. In this tutorial, we’ll embark on a journey through the fascinating realm of General-Purpose GPU Computing, with a special focus on CUDA.
What is CUDA?
- The Compute Unified Device Architecture (CUDA), is a parallel computing platform and application programming interface (API) developed by NVIDIA. It’s a technology that allows you to use your GPU for more than just rendering graphics in games or applications.
- CUDA opens the door to leveraging the immense power of your GPU for handling complex tasks in our increasingly parallel computing world. Its capability to substantially speed up computations makes it indispensable in a wide array of domains, including scientific research, machine learning, and many others.
GPU vs. CPU: The Powerhouse Showdown
To truly grasp the significance of CUDA, it’s essential to understand the fundamental differences between GPUs and CPUs. Think of your CPU as the conductor of a symphony, leading one instrument at a time through a musical masterpiece. CPUs are designed for serial processing, excelling in tasks that require executing instructions one after the other. They’re your go-to for everyday computing, such as browsing the web and multitasking efficiently. But when it comes to highly parallel workloads, CPUs can hit performance bottlenecks.
In contrast, GPUs are the rockstars of parallelism. Imagine a grand orchestra with thousands of specialized musicians playing in harmony. That’s what GPU parallelism looks like. This architecture excels at handling multiple threads in parallel, making it ideal for data-parallel and compute-intensive tasks. From scientific simulations to image processing and deep learning, GPUs take complex problems and break them into smaller, parallel tasks for astonishing speed gains.
The Allure of GPU Acceleration: Why You Should Care?
So, why should you be excited about GPU acceleration and learning CUDA? There are plenty of reasons:
Unbelievable Speed: GPU parallelism can transform your applications, completing tasks that used to take hours or days on a CPU in mere minutes or seconds.
Data Handling Power: GPUs excel at efficiently processing large datasets, making them invaluable for data analysis, mining, and visualization.
Ready to Scale: With GPUs, you can easily scale up your system’s performance by adding more GPUs, providing additional computational power as needed.
Energy-Efficient Performance: GPUs often outperform CPUs in terms of energy efficiency, offering substantial computational power while conserving energy, making them cost-effective and eco-friendly.
Versatility: GPU acceleration isn’t limited to a specific domain. It’s a versatile tool, adaptable to fields ranging from scientific research and healthcare to financial modeling and gaming.
What is Parallel Computing?
Parallel computing in CUDA C++ is a fundamental concept that enables the simultaneous execution of multiple operations or tasks. Imagine dealing with a substantial computational workload, like processing large datasets or conducting intricate simulations. Instead of handling each part one after the other, parallel computing divides the work into smaller, independent units. These units are processed concurrently, allowing for a substantial boost in computational speed and efficiency.
In CUDA, you have two main types of parallel computing:
- Task Parallelism: Task parallelism occurs when numerous tasks or functions can be executed independently and largely concurrently. It revolves around distributing functions across multiple cores.
- Data Parallelism: On the other hand, data parallelism occurs when there are numerous data items that can be processed simultaneously, emphasizing the distribution of data across multiple cores.
Heterogeneous Computing
Heterogeneous computing is a fundamental paradigm that involves the strategic use of diverse processing units within a single computational system. This approach aims to maximize computational efficiency by combining different types of processors, typically CPUs (Central Processing Units) and GPUs (Graphics Processing Units), each with its unique strengths. A heterogeneous application consists of two parts:
Host Code (CPU): The Host Code runs on the CPU and manages high-level tasks and decisions. It’s like the “manager” of the system, coordinating data transfers and task execution.
Device Code (GPU): Device Code is executed on the GPU, leveraging its parallel processing capabilities. It uses specialized functions (kernels) to perform parallel operations, with many threads working together to process data concurrently. This makes the GPU a potent parallel processor.
Computer Architecture
In computer architecture, Flynn’s Taxonomy is a foundational classification system for understanding and categorizing computer architectures. It defines how instructions and data flow within computational cores. It consists of four distinct categories, each with unique characteristics:
- Single Instruction Single Data (SISD): One processor executes a single instruction stream on a single data stream, characteristic of most traditional, sequential computing systems.
- Single Instruction Multiple Data (SIMD): A single instruction is applied to multiple data elements simultaneously, a fundamental concept in parallel computing, particularly in GPUs used in CUDA.
- Multiple Instruction Single Data (MISD): Multiple instructions act on a single data stream, found in specialized systems.
- Multiple Instruction Multiple Data (MIMD): Multiple instructions operate on multiple data streams concurrently, common in multi-core processors and distributed computing systems.
Setting Up Your Development Environment
When getting started with CUDA programming, you have several options for your development environment. You can choose to work on your local machine using integrated development environments (IDEs) like Visual Studio Code, Eclipse, NVIDIA Nsight Eclipse or you can utilize cloud-based resources like Google Colab with GPU support.
Local Machine with Visual Studio Code/ Eclipse/NVIDIA Nsight Eclipse:
- Setting up CUDA on your local machine involves installing the necessary CUDA Toolkit and GPU drivers.
- Once that’s done, you can use CUDA C++ extensions available for popular IDEs like Visual Studio Code, Eclipse, or NVIDIA Nsight Eclipse.
- These extensions provide features such as syntax highlighting, code completion, and integrated debugging, making it easier to write and test CUDA programs locally.
Google Colab with GPU
- Google Colab offers a cloud-based environment with GPU support, allowing you to run CUDA programs without needing a dedicated GPU on your local machine.
- You can create Colab notebooks and write CUDA C++ code directly within the notebook cells. By selecting a GPU runtime, you can harness the power of GPUs for parallel processing.
Writing The First CUDA Program
Absolutely, learning a new programming language, including CUDA C++, is best done by writing programs. Let’s break down how to execute a simple “Hello, World!” program using CUDA C++ into various steps.
- Write the CUDA Kernel: Let us use the Google Colab and write a CUDA kernel within a code cell in the Colab notebook. We need to use %%cu at the beginning of the cell to indicate that it contains a CUDA code.
- The __global__ keyword is used to declare a function known as GPU kernel.
- When you mark a function with __global__, it means that this function will be executed on the GPU (device) and can be launched from the CPU (host).
%%cu
#include <iostream>
__global__ void helloWorld() {
printf("Hello, World from thread %d!\n", threadIdx.x);
}
- Implement the Main Function: In a separate code cell within the Colab notebook, let us implement a main function and the code for launching the CUDA kernel.
%%cu
int main() {
helloWorld<<<1, 10>>>();
cudaDeviceSynchronize();
return 0;
}
- The output of the code described above will be “Hello, World” messages from the GPU threads. Specifically, you’ll see ten “Hello, World” messages, each one indicating the thread number, like this:
Output:
Hello, World from thread 0!
Hello, World from thread 1!
Hello, World from thread 2!
Hello, World from thread 3!
Hello, World from thread 4!
Hello, World from thread 5!
Hello, World from thread 6!
Hello, World from thread 7!
Hello, World from thread 8!
Hello, World from thread 9!
CUDA Programming Model
The CUDA programming model is designed for parallel computing and assumes a system with both a host (usually a CPU) and a device (typically a GPU), each having its own separate memory. It enables developers to allocate, manage, and efficiently transfer data between host and device memory, facilitating high-performance, data-parallel operations on the GPU. Let’s delve into the essential concepts that underlie the CUDA programming model.
CUDA Execution Sequence
The typical processing flow of a CUDA program involves three fundamental steps:
Data Transfer: Data is copied from CPU memory to GPU memory. This step is crucial for preparing the data for parallel processing on the GPU.
Kernel Invocation: Kernels, parallelizable functions, are invoked to perform operations on the data stored in GPU memory. Kernels define tasks that run concurrently on the GPU, harnessing the power of parallelism.
Data Retrieval: After GPU computations are complete, the results are copied back from GPU memory to CPU memory. This step ensures that the processed data is readily accessible for further analysis or utilization on the CPU.
Managing Memory
In the CUDA programming model, effective memory management plays a crucial role. It encompasses vital functions such as cudaMalloc, cudaMemcpy, cudaMemset, and cudaFree. let us discuss them one by one.
- cudaMalloc: The cudaMalloc is the equivalent of malloc for CPU memory, but it operates in the GPU’s device memory. It allows you to allocate a specified amount of memory on the GPU and returns a pointer to the allocated memory. Here’s an example:
int* d_data; // Pointer for device memory
int size = 100 * sizeof(int); // Allocate space for 100 integers
cudaMalloc((void**)&d_data, size); // Allocate memory on the GPU
- cudaMemcpy: It is used to move data between the CPU (host) and GPU (device) and vice versa. In the example below, cudaMemcpyHostToDevice is used to copy data from the host to the device, and cudaMemcpyDeviceToHost is used to copy data from the device to the host.
int h_data[] = {1, 2, 3, 4, 5};
int* d_data;
int dataSize = sizeof(h_data);
// Allocate memory on the GPU
cudaMalloc((void**)&d_data, dataSize);
// Copy data from host to device
cudaMemcpy(d_data, h_data, dataSize, cudaMemcpyHostToDevice);
// Perform GPU operations with d_data
// Copy results back from device to host
cudaMemcpy(h_data, d_data, dataSize, cudaMemcpyDeviceToHost);
- cudaMemset: It is used to initialize or clear device memory. It allows developers to set a specified value across a block of memory in the GPU.
int size = 5 * sizeof(int);
int* d_data;
// Utilize cudaMemset to set all elements in the deviceArray to 0
cudaMemset(d_data, 0, size);
- cudaFree: It is used to deallocate memory that was previously allocated on the GPU using cudaMalloc. It is essential to free memory resources on the GPU to ensure efficient memory management.
// Deallocate the assigned memory using cudaFree
cudaFree(d_data);
Thread Hierarchy
In CUDA programming, understanding the concept of thread hierarchy is fundamental. It forms the backbone of how you organize and utilize parallelism on the GPU. This section will introduce you to the core elements of thread hierarchy in CUDA.
Why Thread Hierarchy Matters?
Thread hierarchy isn’t just a technical detail; it’s a vital component for achieving the best GPU performance. Here’s why understanding thread hierarchy is essential:
Efficient Parallelism: Thread hierarchy is the key to efficiently managing parallel tasks on GPUs. It allows you to take full advantage of the GPU’s parallel processing power.
Resource Optimization: Properly organizing threads ensures the GPU’s resources are used effectively. This efficient usage leads to faster application execution and maximizes the GPU’s potential.
Optimization Opportunities: Thread hierarchy forms the basis of CUDA program optimization. By configuring threads, blocks, and grids thoughtfully, you can tailor your application to your problem’s parallelism requirements and the GPU’s architecture.
Error Prevention: Understanding thread hierarchy is crucial for avoiding common programming mistakes. Well-organized threads help prevent issues and performance bottlenecks, resulting in robust and reliable code.
Threads, Blocks, and Grids
In the CUDA programming model, threads, blocks, and grids are the building blocks that enable you to harness the power of GPU parallelism effectively. Understanding how these elements work together is essential for optimizing your CUDA programs. This section will delve into the definitions and usage of threads, blocks, and grids, helping you visualize the hierarchical structure that is fundamental to CUDA programming.
Defining Threads
Threads are the smallest units of computation within CUDA. They are organized within blocks, and each thread runs a specific portion of the code. Threads are executed concurrently on SMs, and the order of execution might vary due to parallelism.
Organizing Threads into Thread Blocks
Thread blocks are the intermediate level in the hierarchy. Each thread block is a group of threads that can collaborate and share data through fast shared memory. Thread blocks are organized within grids and are assigned to different streaming multiprocessors (SMs) on the GPU. Each SM can execute multiple thread blocks, depending on its capacity.
Creating Grids of Blocks
A grid is the highest level of the thread hierarchy. It represents a collection of thread blocks. A grid can contain a massive number of thread blocks, which, in turn, can contain numerous threads. The concept of a grid allows you to manage a vast number of threads efficiently. The figure below shows pictorial representation of thread hierarchy involving threads, thread blocks and grids.
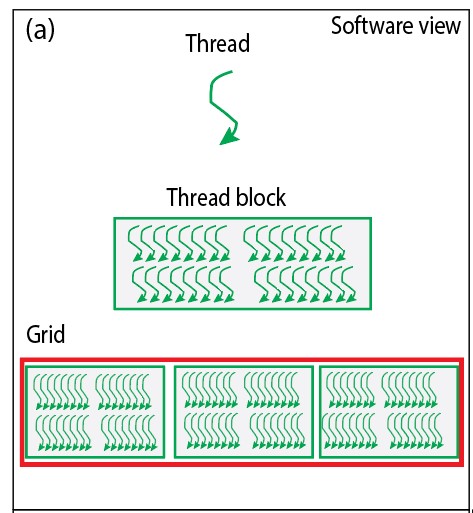
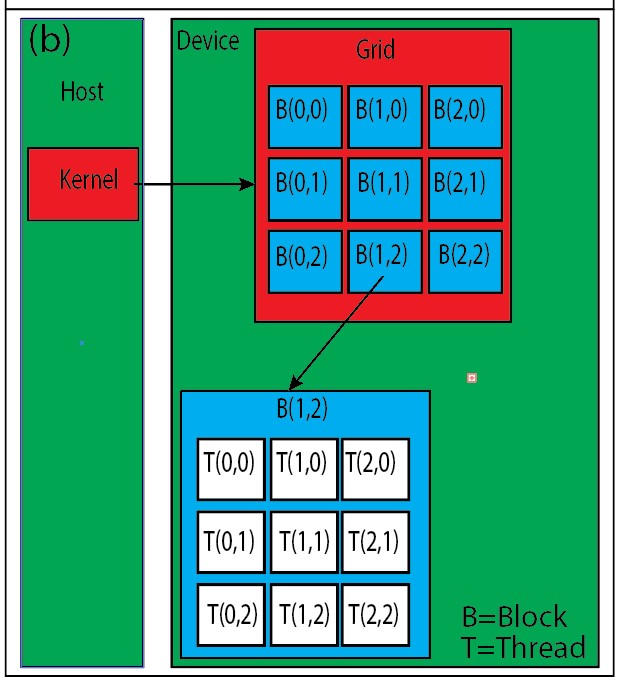
Fig. Pictorial representaion of threads, threadblocks and grids
Thread Indexing
Thread indexing is used to manage and identify individual threads in a parallel computing environment. To identify individual threads in this hierarchy, CUDA provides built-in variables blockIdx and threadIdx. These variables are accompanied by .x, .y, and .z components for working in three-dimensional thread spaces. The blockIdx.x represents the index of the current block within the grid in the x-direction. The threadIdx.x represents the index of the current thread within its block in the x-direction.
Calculating Thread Identifiers In One Dimension
Once we understand threadIdx and blockIdx, we can leverage them to determine a thread’s global index. This global index tells us where a thread is located in the entire grid of blocks and threads. To determine the global index (unique identifier) of a thread, CUDA programmers often use an expression like this:
int tid = blockIdx.x * blockDim.x + threadIdx.x;
Here’s how this calculation works:
- blockIdx.x is the index of the block within the grid.
- blockDim.x is the number of threads per block (block dimension).
- threadIdx.x is the index of the thread within its block.
By multiplying the index of the block by the number of threads per block (blockIdx.x * blockDim.x) and adding the index of the thread within its block (threadIdx.x), you get a unique thread identifier tid. This helps distinguish one thread from another and plays a crucial role in determining the specific task each thread should execute.
Illustrative Example Of Thread Identification
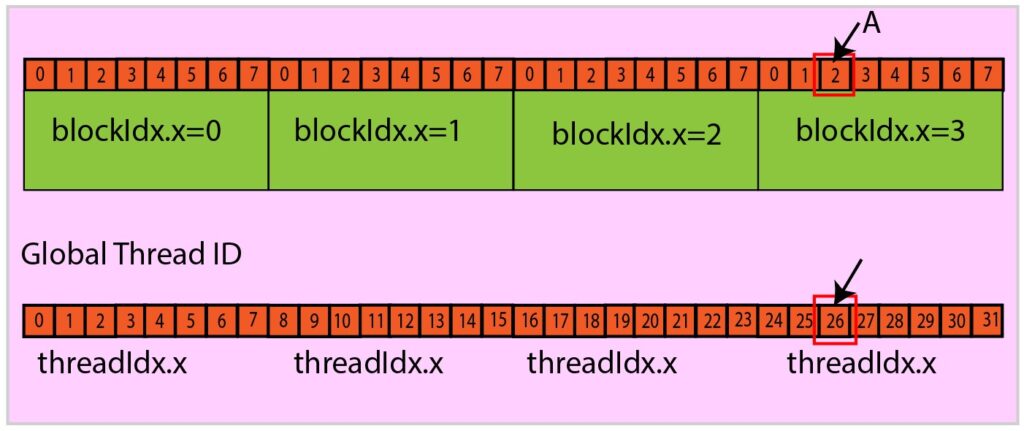
Consider a hypothetical setup with a one-dimensional grid and one-dimensional blocks: there are 4 blocks, and each block consists of 8 threads.
Let us try to compute the global thread ID of thread A as indicated in the figure. For the thread A:
- threadIdx.x=2, blockidx.x=3, blockDim.x=8.
- Global Thread ID = blockIdx.x * blockDim.x + threadIdx.x= 3 x 8 + 2 = 26
Calculating Thread Identifiers In Two Dimensions
In CUDA, we often work with data structures that have two-dimensional or multidimensional characteristics. Calculating thread identifiers in two dimensions is crucial for effectively partitioning and processing such data. To calculate the global thread identifier or thread index in two dimensions, we can use the following formula:
int tid_x = blockIdx.x * blockDim.x + threadIdx.x;
int tid_y = blockIdx.y * blockDim.y + threadIdx.y;
In the above formula:
- blockIdx.x specifies which block the thread belongs to along the x-axis.
- blockDim.x is the number of threads within each block along the x-axis, indicating the block’s width.
- threadIdx.x is the local thread index within the block along the x-axis.
- blockIdx.y specifies which block the thread belongs to along the y-axis.
- blockDim.y is the number of threads within each block along the y-axis, representing the block’s height.
- threadIdx.y is the local thread index within the block along the y-axis.
Writing a CUDA Kernel
A CUDA kernel function serves as the foundation for GPU computation, specifying operations to be performed by individual threads and their data access patterns. When the kernel is invoked, multiple threads execute these computations in parallel. Kernels are defined using the global declaration specifier, as demonstrated below.
__global__ void kernel_name(argument list)
Here’s a simple example of a CUDA kernel that sums two arrays:
__global__ void addArrays(int* a, int* b, int* result, int size) {
int tid = blockIdx.x * blockDim.x + threadIdx.x;
if (tid < size) {
result[tid] = a[tid] + b[tid];
}
}
Explanation:
- The kernel is named addArrays, and it is defined with the __global__ specifier, indicating that it will be executed on the GPU device.
- The kernel takes four arguments: pointers to arrays a, b, and result, as well as an integer size, which specifies the number of elements to process.
- Within the kernel, each thread calculates its unique identifier tid by combining the blockIdx.x, representing the block index, and threadIdx.x, representing the thread index within the block. This identifier helps determine the element each thread will operate on.
- If the tid is within the specified size, the thread adds the corresponding elements from arrays a and b and stores the result in the result array at the same index.
Lunching a CUDA Kernel
A CUDA kernel can be launched from the host side using the following syntax:
kernel_name<<<dimGrid, dimBlock>>>(kernel_arguments);
In the above syntax:
- kernel_name is the name of the kernel function.
- dimGrid specifies the number of blocks in the grid.
- dimBlock determines the number of threads per block.
- kernel_arguments represents any arguments required by the kernel function.
Learning CUDA Through Coding
The most effective approach to learning CUDA is through practical coding. Let us delve into hands-on exercises to gain a deeper understanding of this parallel computing framework.
Example 1:Summation of Two Arrays Using CUDA
#include <iostream>
using namespace std;
#define N 1000
#define BLOCK_DIM 256
// CUDA kernel to add two arrays
__global__ void arraySum(int *a, int *b, int *c)
{
int idx = threadIdx.x + blockIdx.x * blockDim.x;
if (idx < N)
{
c[idx] = a[idx] + b[idx];
}
}
int main()
{
// Host arrays for input and output
int* h_a = (int*)malloc(N * sizeof(int));
int* h_b = (int*)malloc(N * sizeof(int));
int* h_c = (int*)malloc(N * sizeof(int));
int* h_sum = (int*)malloc(N * sizeof(int));
// Initialize host arrays
for (int i = 0; i < N; i++)
{
h_a[i] = i;
h_b[i] = i;
h_sum[i] = h_a[i] + h_b[i];
}
// Device arrays for input and output
int *d_a;
int *d_b;
int *d_c;
cudaMalloc((void**)&d_a, N * sizeof(int));
cudaMalloc((void**)&d_b, N * sizeof(int));
cudaMalloc((void**)&d_c, N * sizeof(int));
// Copy data from host to device
cudaMemcpy(d_a, h_a, N * sizeof(int), cudaMemcpyHostToDevice);
cudaMemcpy(d_b, h_b, N * sizeof(int), cudaMemcpyHostToDevice);
// Calculate block size and grid size for the CUDA kernel
dim3 dimBlock(BLOCK_DIM);
dim3 dimGrid((N+dimBlock.x-1)/dimBlock.x);
// Launch the CUDA kernel
arraySum<<<dimGrid, dimBlock>>>(d_a, d_b, d_c);
// Copy the result from device to host
cudaMemcpy(h_c, d_c, N * sizeof(int), cudaMemcpyDeviceToHost);
// Output the result
for (int i = 0; i < N; i++)
{
cout << h_c[i] << " ";
}
// Free device and host memory
cudaFree(d_a);
cudaFree(d_b);
cudaFree(d_c);
free(h_a);
free(h_b);
free(h_c);
return 0;
}
Output:
0 2 4 6 8 10 12 14 16 18 20 22 24 26 28 30 32 34 36 38 40 42 44 46 48 50 52 54 56 58 60 62 64 66 68 70 72 74 76 78 80 82 84 86 88 90 92 94 96 98 100 102 104 106 108 110 112 114 116 118 120 122 124 126 128 130 132 134 136 138 140 142 144 146 148 150 152 154 156 158 160 162 164 166 168 170 172 174 176 178 180 182 184 186 188 190 192 194 196 198 200 202 204 206 208 210 212 214 216 218 220 222 224 226 228 230 232 234 236 238 240 242 244 246 248 250 252 254 256 258 260 262 264 266 268 270 272 274 276 278 280 282 284 286 288 290 292 294 296 298 300 302 304 306 308 310 312 314 316 318 320 322 324 326 328 330 332 334 336 338 340 342 344 346 348 350 352 354 356 358 360 362 364 366 368 370 372 374 376 378 380 382 384 386 388 390 392 394 396 398 400 402 404 406 408 410 412 414 416 418 420 422 424 426 428 430 432 434 436 438 440 442 444 446 448 450 452 454 456 458 460 462 464 466 468 470 472 474 476 478 480 482 484 486 488 490 492 494 496 498 500 502 504 506 508 510 512 514 516 518 520 522 524 526 528 530 532 534 536 538 540 542 544 546 548 550 552 554 556 558 560 562 564 566 568 570 572 574 576 578 580 582 584 586 588 590 592 594 596 598 600 602 604 606 608 610 612 614 616 618 620 622 624 626 628 630 632 634 636 638 640 642 644 646 648 650 652 654 656 658 660 662 664 666 668 670 672 674 676 678
Explanation:
- Defines an array size N and block size BLOCK_DIM for the CUDA kernel.
- Initializes host arrays h_a, h_b, h_c, and h_sum and populates them with values.
- Allocates device memory for arrays d_a, d_b, and d_c using cudaMalloc.
- Copies data from host arrays h_a and h_b to device arrays d_a and d_b using cudaMemcpy.
- Calculates grid and block dimensions for launching the CUDA kernel.
- Launches the CUDA kernel arraySum using grid and block dimensions.
- In the kernel function, each thread computes a global index (idx) and checks if it’s within the array size (N) before performing element-wise addition and storing results in d_c.
- Copies results from the device (d_c) back to the host array (h_c) using cudaMemcpy.
- Prints the elements of h_c, displaying the sum of elements from h_a and h_b.
- Releases device memory using cudaFree and host memory using free.
- The main function returns 0 to indicate successful execution.
Example 2: Summation Of Two Matrices Using CUDA
// Add Two Matrices
#include <iostream>
#define N 10
#define M 20
#define BLOCK_DIM 16
using namespace std;
// CUDA kernel to add two matrices
__global__ void matrixAdd(int *a, int *b, int *c)
{
int ix = blockIdx.x * blockDim.x + threadIdx.x;
int iy = blockIdx.y * blockDim.y + threadIdx.y;
int index = ix + iy * N;
if (ix < N && iy < M)
{
c[index] = a[index] + b[index];
}
}
int main()
{
// Define matrix dimensions and block size
int h_a[N][M], h_b[N][M], h_c[N][M];
int *d_a, *d_b, *d_c;
int size = N * M * sizeof(int);
// Initialize host matrices h_a and h_b
for (int i = 0; i < N; i++)
{
for (int j = 0; j < M; j++)
{
h_a[i][j] = 1;
h_b[i][j] = 2;
}
}
// Allocate device memory for matrices
cudaMalloc((void **)&d_a, size);
cudaMalloc((void **)&d_b, size);
cudaMalloc((void **)&d_c, size);
// Copy data from host to device
cudaMemcpy(d_a, h_a, size, cudaMemcpyHostToDevice);
cudaMemcpy(d_b, h_b, size, cudaMemcpyHostToDevice);
// Define the grid and block dimensions
dim3 dimBlock(BLOCK_DIM, BLOCK_DIM);
dim3 dimGrid((N + dimBlock.x - 1) / dimBlock.x, (M + dimBlock.y - 1) / dimBlock.y);
// Launch the kernel to add matrices
matrixAdd<<<dimGrid, dimBlock>>>(d_a, d_b, d_c);
cudaDeviceSynchronize();
// Copy the result from device to host
cudaMemcpy(h_c, d_c, size, cudaMemcpyDeviceToHost);
// Output the result
for (int i = 0; i < N; i++)
{
for (int j = 0; j < M; j++)
{
cout << h_c[i][j] << " ";
}
cout << endl;
}
// Free device memory
cudaFree(d_a);
cudaFree(d_b);
cudaFree(d_c);
return 0;
}
Output:
3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
Explanation:
- The code adds two matrices using parallel processing on a GPU.
- It defines a CUDA kernel function matrixAdd to perform matrix addition element-wise.
- The main function initializes host matrices h_a and h_b with sample values.
- It allocates device memory for matrices d_a, d_b, and d_c.
- Data is transferred from the host to the device using cudaMemcpy.
- Grid and block dimensions are defined to cover the entire matrices.
- The matrixAdd kernel is launched to perform the matrix addition.
- After execution, the result is copied back to the host and printed.
- Device memory is released using cudaFree.
Example 3: Matrix Transpose Using CUDA
// Transpose of a matrix
#include<iostream>
#define N 4
#define M 7
#define block_dim 32
using namespace std;
// CUDA kernel to transpose a matrix
__global__ void matrixTranspose(int *a, int *b)
{
int ix = threadIdx.x + blockIdx.x * blockDim.x;
int iy = threadIdx.y + blockIdx.y * blockDim.y;
int index = ix + iy * N;
int transposed_index = iy + ix * M;
// Check boundaries to avoid out-of-bounds memory access
if (ix < N && iy < M)
{
b[index] = a[transposed_index];
}
}
int main()
{
int h_a[N][M], h_b[M][N];
int *d_a, *d_b;
int size = N * M * sizeof(int);
// Initialize the host matrix h_a
for (int i = 0; i < N; i++)
{
for (int j = 0; j < M; j++)
{
h_a[i][j] = i * j;
}
}
// Allocate device memory for matrices
cudaMalloc((void**)&d_a, size);
cudaMalloc((void**)&d_b, size);
// Copy data from host to device
cudaMemcpy(d_a, h_a, size, cudaMemcpyHostToDevice);
// Define grid and block dimensions
dim3 dimBlock(block_dim, block_dim);
dim3 dimGrid((N + dimBlock.x - 1) / dimBlock.x, (M + dimBlock.y - 1) / dimBlock.y);
// Launch the kernel to transpose the matrix
matrixTranspose<<<dimGrid, dimBlock>>>(d_a, d_b);
cudaDeviceSynchronize();
// Copy the result from device to host
cudaMemcpy(h_b, d_b, size, cudaMemcpyDeviceToHost);
cout << "Matrix=>" << endl;
for (int i = 0; i < N; i++)
{
for (int j = 0; j < M; j++)
{
cout << h_a[i][j] << " ";
}
cout << endl;
}
cout << "Transposed Matrix=>" << endl;
for (int i = 0; i < M; i++)
{
for (int j = 0; j < N; j++)
{
cout << h_b[i][j] << " ";
}
cout << endl;
}
// Free device memory
cudaFree(d_a);
cudaFree(d_b);
return 0;
}
Output:
Matrix=>
0 1 2 3 4 5 6
1 2 3 4 5 6 7
2 3 4 5 6 7 8
3 4 5 6 7 8 9
Transposed Matrix=>
0 1 2 3
1 2 3 4
2 3 4 5
3 4 5 6
4 5 6 7
5 6 7 8
6 7 8 9
Cuda Execution Model
The CUDA execution model provides a way of thinking about how modern NVIDIA GPUs achieve parallel computing. This model reveals the underlying principles that make GPU parallelism possible and allows developers to design efficient, high-performance applications. So, it’s not just a theoretical concept but a practical guide to unleashing the full potential of GPU computing. In the following subsections, we will discuss CUDA execution model in detail.
Logical View Of CUDA Programming
The Logical View of CUDA Programming offers a high-level, abstract perspective on the principles and concepts behind GPU-accelerated parallel computing. It focuses on fundamental concepts such as parallel threads, synchronization, memory hierarchy, data parallelism, and scalability, providing a conceptual framework for understanding CUDA development. This view is essential for grasping the design paradigms and strategies needed to harness the parallel computing power of NVIDIA GPUs effectively. Developers can use the Logical View to plan the architecture and parallelism of their applications without delving into low-level hardware details.
Hardware View Of CUDA Programming
The Hardware View of CUDA Programming offers an in-depth understanding of the underlying GPU architecture and hardware components that execute CUDA code. It delves into details such as the organization of Streaming Multiprocessors (SMs), memory hierarchies, and the execution of CUDA threads at the hardware level. This view is essential for optimizing CUDA programs, as it provides insights into memory management, thread execution, and resource allocation within the GPU. The below shows pictorial representation of hardware and software view of CUDA programming.
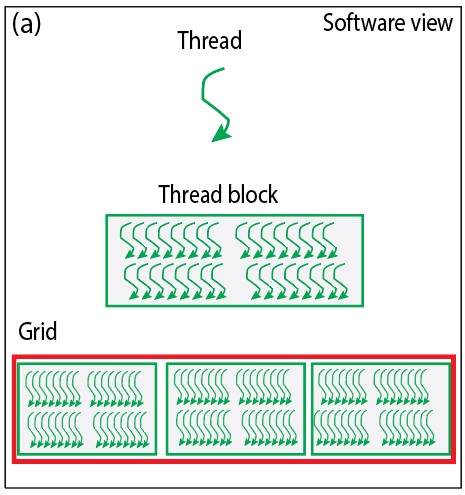
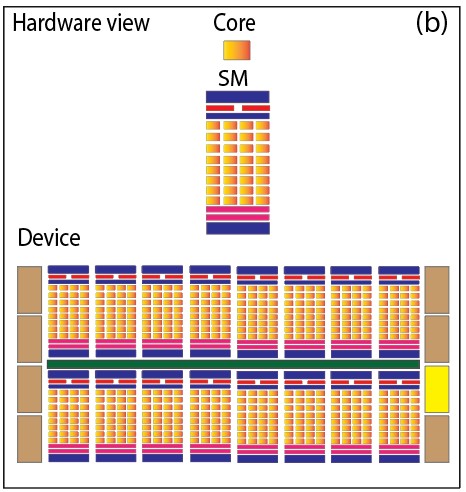
Fig. Software and hardware view of CUDA programming
GPU Architecture Overview
- Understanding GPU architecture is essential for CUDA programming because it enables efficient utilization of the hardware’s parallelism, memory hierarchy, and resources, leading to optimal performance gains and effective debugging.
- The GPU’s architecture is structured around a flexible array of Streaming Multiprocessors (SM), which is the fundamental unit for harnessing hardware parallelism. The figure below shows the key components of a Fermi SM.
Streaming Multiprocessor (SM)
- Each Streaming Multiprocessor (SM) in a GPU is designed to support concurrent execution of hundreds of threads.
- There are typically multiple SMs within a single GPU.
- When a kernel grid is launched, the thread blocks within that grid are distributed across the available SMs for execution.
- Each SM takes on the responsibility of executing the threads from one or more thread blocks.
- Threads within a thread block execute concurrently, but only on the assigned SM.
- Once scheduled on an SM, all threads in a thread block execute on that SM.
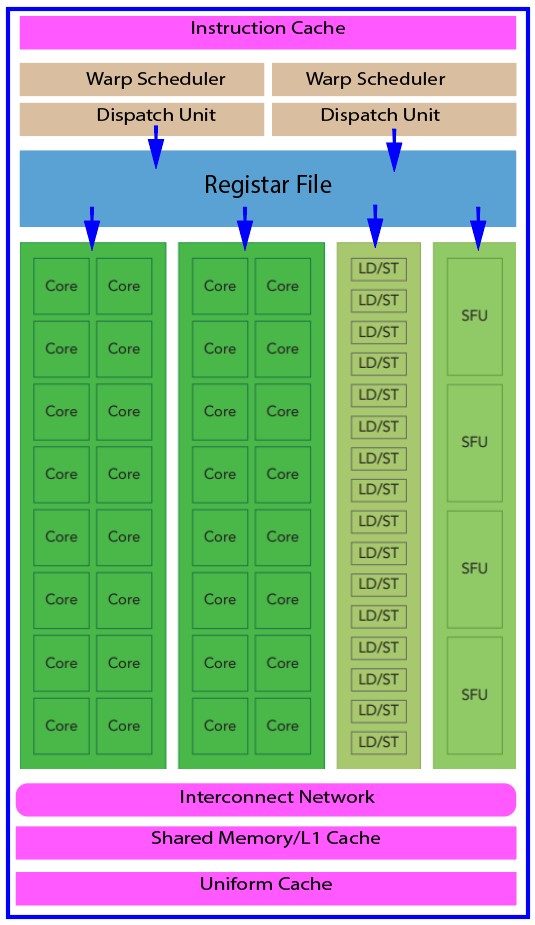
Fig. Key components of Fermi SM.
Let us discuss the key components of the Fermi SM shown above:
- CUDA Cores: At the heart of the SM are the CUDA Cores, which are the workhorses responsible for performing the actual computation. These cores execute instructions concurrently, enabling the parallel processing capabilities of the GPU. With each new GPU generation, the number of CUDA Cores within an SM has significantly increased, enhancing the overall computational power.
- Shared Memory/L1 Cache: Shared memory, often referred to as L1 cache, serves as a high-speed memory space that is shared among threads within a block. This memory is utilized for temporary data storage and is particularly valuable for data sharing among threads. Efficient use of shared memory is essential for optimizing performance in parallel algorithms. It acts as a buffer that reduces the time it takes to access data compared to fetching it from slower global memory.
- Register File: Registers are tiny, ultra-fast memory storage units that play a crucial role in GPU computation. Each thread within a CUDA block has its own set of registers to hold thread-specific data. Registers are used to store variables, intermediate results, and other essential data. As registers are much faster to access than shared or global memory, they contribute to the overall speed and efficiency of the GPU’s parallel processing.
- Load/Store Units (LD/ST): Load and store units are responsible for data transfers between global memory and the SM. Global memory is the largest and slowest memory in the GPU hierarchy, so efficiently managing data movement between global memory and the SM is critical for performance optimization. Load units fetch data from global memory, while store units write data back to it. Efficient memory access patterns and memory hierarchy management are crucial to minimizing data transfer overhead.
- Special Function Units (SFU): Special Function Units (SFUs) are specialized hardware units within the SM that handle various mathematical and logical operations. These include operations like sine, cosine, and square root calculations, as well as logical operations like bitwise AND, OR, and XOR. SFUs significantly accelerate the execution of specific operations, especially in applications that heavily rely on trigonometric functions or advanced mathematical computations.
- Warp Scheduler: The Warp Scheduler is a critical component responsible for orchestrating the execution of threads within an SM. Threads are grouped into units known as warps. These warps are typically composed of 32 threads. The Warp Scheduler schedules the warps to ensure that they are executed efficiently, managing thread execution, and handling latency by switching to different warps when waiting for data. This dynamic scheduling is essential for hiding memory access latencies and maximizing SM utilization.
Single Instruction Multiple Threads (SIMT)
- SIMT, or Single Instruction, Multiple Threads, is a parallel execution model used in modern GPU (Graphics Processing Unit) architectures.
- In the SIMT model, a large number of threads work concurrently, executing the same instruction stream, but they can diverge along different execution paths based on conditional statements.
- This flexibility allows SIMT to efficiently handle tasks with diverse data and conditional requirements, making it well-suited for applications like graphics rendering, simulations, and parallel computing.
- SIMT is a key feature of GPU computing, enabling high levels of parallelism and computational efficiency.
Example of SIMT
- Imagine a classroom where a teacher hands out math worksheets to students. Each student receives a unique pair of numbers, and the task is to find the product of those two numbers.
- The teacher provides the same set of multiplication instructions to all students, and they execute these instructions independently using their individual number pairs.
- Additionally, the teacher instructs the students that if one of the numbers is negative, they should perform a subtraction instead of multiplication.
- In this scenario, the teacher’s instructions represent a single instruction (SIMT model), and the students execute these instructions concurrently but with different data (their unique number pairs) and some variation in execution based on the provided rule. This reflects the SIMT execution model found in GPUs, where multiple threads execute the same instruction but with divergent control flow when needed.
Why SIMT is Different from SIMD?
SIMT (Single Instruction, Multiple Threads) and SIMD (Single Instruction, Multiple Data) are both parallel execution models, but they exhibit distinct characteristics that set them apart in the world of parallel computing. Understanding these differences is essential for optimizing GPU programming.
Control Flow Flexibility:
- In SIMT, threads within the same warp (a group of threads that execute in lockstep) can follow different control flow paths based on conditional statements. This flexibility allows each thread to make independent decisions during execution.
- In contrast, SIMD mandates that all threads adhere to the same control flow path, which can be limiting when dealing with diverse conditional scenarios.
Divergent Execution:
- SIMT accommodates divergent execution, where threads within a warp can execute different code branches. This feature is particularly useful when threads encounter conditional statements, as it ensures that each thread proceeds according to its specific conditions.
- SIMD, on the other hand, struggles with divergence. When some threads within a group follow a different code branch, SIMD requires these threads to wait for the others, resulting in suboptimal performance.
Flexibility in Thread Management:
- SIMT allows dynamic thread management, with threads entering and exiting warps as needed. This adaptability optimizes resource utilization and contributes to better load balancing.
- SIMD has fixed-size vectors, and threads are statically allocated to these vectors. This rigidity can lead to inefficient resource usage and a less adaptable execution model.
Applicability to Real-World Scenarios:
- SIMT is well-suited for applications with varying execution paths, such as image processing, scientific simulations, and machine learning. Its ability to handle diverse and dynamic conditions makes it an excellent choice for these workloads.
- SIMD shines in scenarios where all threads perform the same operations on large datasets simultaneously, such as in multimedia processing or certain scientific computations. However, it may struggle in applications requiring conditional execution.
What is Warp?
- A warp is a group of threads that execute instructions in a coordinated manner. These threads operate in a SIMT (Single Instruction, Multiple Threads) fashion, meaning that they execute the same instruction simultaneously.
- In modern NVIDIA GPU architectures, a warp typically consists of 32 threads. This means that there are 32 threads in a warp, and all of them execute the same instruction at the same time.
Relationship Between Warps and Thead blocks
- When a kernel is launched, the GPU scheduler groups threads into warps. If the total number of threads in a thread block is not a multiple of the warp size (e.g., 32 threads), some warps may be only partially filled.
- Warps are the units that the GPU scheduler uses to issue instructions to the execution units. Each warp is scheduled on a streaming multiprocessor (SM) for execution.
- Threads within a warp execute in SIMT fashion, meaning they execute the same instruction at the same time but with different data. While threads within a warp execute the same instruction, different warps can execute different instructions.
- The Figure below illustrates how the logical view and hardware view of a thread block are connected
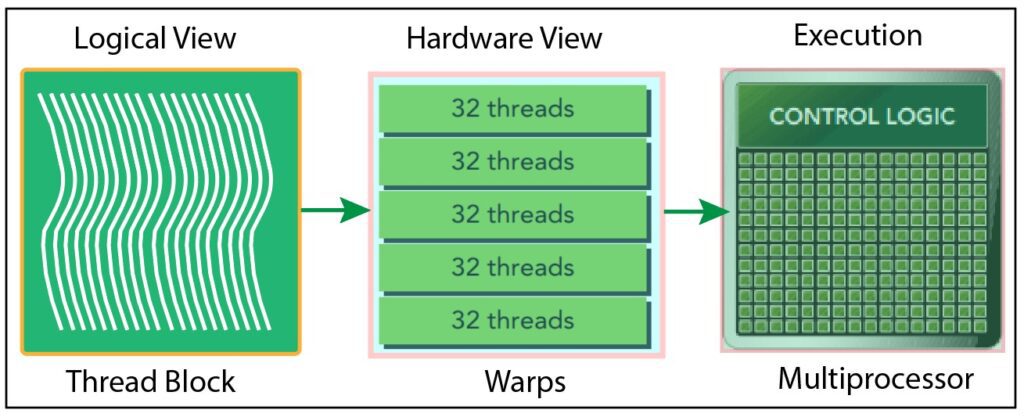
Fig.1. Logical view and hardware view of a thread block
Warp Divergence
In CUDA, a warp is a fundamental unit of thread execution. It’s essentially a group of threads that are executed together in lockstep. This lockstep execution is a key feature of warp and GPU architecture. When all threads in a warp perform the same instruction simultaneously, it maximizes parallelism and ensures efficient GPU operation.
However, warp divergence occurs when some threads within a warp need to take different paths due to conditional statements in your code. For example, consider the following statement:
if (cond) {
// Code block A
} else {
// Code block B
}
If half the threads in a warp go down “Code block A” while the other half goes down “Code block B,” this is where divergence happens. If threads of a warp diverge, the warp serially executes each branch path, disabling threads that do not take that path.
The key consequence of warp divergence is that it leads to inefficiencies in GPU execution. Because threads within a warp are supposed to be in lockstep, if they diverge, it means they can no longer execute in perfect parallel. Instead, they become serialized, meaning they execute one after the other. This can significantly slow down your CUDA program’s performance. Let us try to understand warp divergence with the help of a code:
#include <iostream>
using namespace std;
const int N = 64;
const int warpSize = 32;
__global__ void warpDivFunction(float* c) {
int tid = blockIdx.x * blockDim.x + threadIdx.x;
float a, b;
a = b = 0.5f;
// Check for warp divergence
if (tid % 2 == 0) {
a = 1.0f; // Threads with even thread IDs set 'a'
} else {
b = 100.0f; // Threads with odd thread IDs set 'b'
}
c[tid] = a + b;
}
int main() {
float* h_c = new float[N];
float* d_c;
// Allocate device memory for the result
cudaMalloc((void**)&d_c, N * sizeof(float));
// Launch the warpDivFunction kernel with N threads
warpDivFunction<<<1, N>>>(d_c);
// Copy the result back to the host
cudaMemcpy(h_c, d_c, N * sizeof(float), cudaMemcpyDeviceToHost);
// Print the result
for (int i = 0; i < N; ++i) {
cout << h_c[i] << " ";
}
// Clean up allocated memory
delete[] h_c;
cudaFree(d_c);
return 0;
}
Output:
1.5 100.5 1.5 100.5 1.5 100.5 1.5 100.5 1.5 100.5 1.5 100.5 1.5 100.5 1.5 100.5 1.5 100.5 1.5 100.5 1.5 100.5 1.5 100.5 1.5 100.5 1.5 100.5 1.5 100.5 1.5 100.5 1.5 100.5 1.5 100.5 1.5 100.5 1.5 100.5 1.5 100.5 1.5 100.5 1.5 100.5 1.5 100.5 1.5 100.5 1.5 100.5 1.5 100.5 1.5 100.5 1.5 100.5 1.5 100.5 1.5 100.5 1.5 100.5
Explanation:
- The code defines a CUDA kernel function named warpDivFunction that operates on an array c. It’s designed to illustrate warp divergence. Each thread, identified by its tid (thread ID), initializes two float variables a and b with values of 0.5.
- Within the kernel, a check for warp divergence is implemented using if (tid % 2 == 0). When tid is even (threads with even thread IDs), it sets a to 1.0f, and when tid is odd (threads with odd thread IDs), it sets b to 100.0f. This demonstrates that threads within the same warp might execute different instructions, leading to warp divergence.
- In the main function, the code allocates memory for the result on the device, launches the warpDivFunction kernel with N threads, copies the result back to the host, and prints the values to the console.
- The main takeaway here is that when threads within a warp take different code paths, it can lead to inefficiencies due to serialization of execution, which can impact the overall performance of a CUDA application.
However, it is possible to avoid warp divergence using a warp-centric approach that achieves 100 percent utilization of the device. In the warp-centric approach, we need to use (tid / warpSize) % 2 == 0) instead of (tid % 2 == 0). Let us examine the code below that uses a warp-centric approach.
#include <iostream>
using namespace std;
const int N = 64;
const int warpSize = 32;
__global__ void warpDivFunction(float* c) {
int tid = blockIdx.x * blockDim.x + threadIdx.x;
float a, b;
a = b = 0.5f;
// Check for warp divergence
if ((tid / warpSize) % 2 == 0) {
a = 1.0f; // Threads in even warps set 'a'
} else {
b = 100.0f; // Threads in odd warps set 'b'
}
c[tid] = a + b;
}
int main() {
float* h_c = new float[N];
float* d_c;
// Allocate device memory for the result
cudaMalloc((void**)&d_c, N * sizeof(float));
// Launch the warpDivFunction with N threads
warpDivFunction<<<1, N>>>(d_c);
// Copy the result back to the host
cudaMemcpy(h_c, d_c, N * sizeof(float), cudaMemcpyDeviceToHost);
// Print the result
for (int i = 0; i < N; ++i) {
cout << h_c[i] << " ";
}
// Clean up allocated memory
delete[] h_c;
cudaFree(d_c);
return 0;
}
Output:
1.5 1.5 1.5 1.5 1.5 1.5 1.5 1.5 1.5 1.5 1.5 1.5 1.5 1.5 1.5 1.5 1.5 1.5 1.5 1.5 1.5 1.5 1.5 1.5 1.5 1.5 1.5 1.5 1.5 1.5 1.5 1.5 100.5 100.5 100.5 100.5 100.5 100.5 100.5 100.5 100.5 100.5 100.5 100.5 100.5 100.5 100.5 100.5 100.5 100.5 100.5 100.5 100.5 100.5 100.5 100.5 100.5 100.5 100.5 100.5 100.5 100.5 100.5 100.5
Explanation
- The code defines a CUDA kernel function named warpDivFunction intended to demonstrate warp divergence.
- It operates on an array c and initializes two float variables, a and b, to 0.5 for each thread. It then calculates a unique tid (thread ID) for each thread based on its block and thread indices.
- Within the kernel, the code checks for warp divergence using the condition if ((tid / warpSize) % 2 == 0). If this condition is met (even thread IDs), it sets a to 1.0f, and if it’s not met (odd thread IDs), it sets b to 100.0f.
- In the main function, the code allocates memory for the result on the GPU, launches the warpDivFunction kernel with N threads, copies the result back to the host, and prints the computed values.
- The condition (tid / warpSize) % 2 == 0 ensures that branching aligns with warp-sized segments, resulting in even warps executing the “if” clause while odd warps follow the “else” clause. This approach establishes branch granularity in multiples of the warp size.
Resource Partitioning
Resource partitioning in a GPU primarily involves the allocation and management of two crucial hardware resources: registers and shared memory. These resources play a fundamental role in how parallel tasks are executed on a GPU, and efficiently managing them is key to achieving optimal performance in parallel computing. Let us discuss them one by one.
Registers:
- Registers are small, high-speed memory locations within the GPU. Each thread within a thread block is allocated a certain number of registers for storing local variables and data. However, the total number of registers available per thread block is limited by the GPU’s architecture.
- If threads consume a more number of registers, it can limit the number of active threads within a thread block.
- When each thread consumes fewer registers, more warps can be placed on an SM (Fig. a). While fewer warps can be placed on an SM if there are more registers per thread (Fig. b).
- Optimizing register usage is important to maximize the number of active threads and achieve better parallelism, ultimately leading to improved GPU performance.
Shared Memory:
- Shared memory is a fast, on-chip memory space available in each multiprocessor (SM) of a GPU. It is used for communication and data sharing among threads within the same thread block.
- Like registers, the amount of shared memory available is limited for each SM. If each thread block consumes a small amount of shared memory, it can increase the number of thread blocks that an SM can accommodate (Fig.c).
- When a thread block consumes more shared memory, fewer thread blocks are processed simultaneously by an SM. This can lead to underutilization of the GPU’s resources (Fig.d).
- Effective management of shared memory is vital to ensure that multiple thread blocks can coexist on an SM, maximizing parallelism and GPU performance.
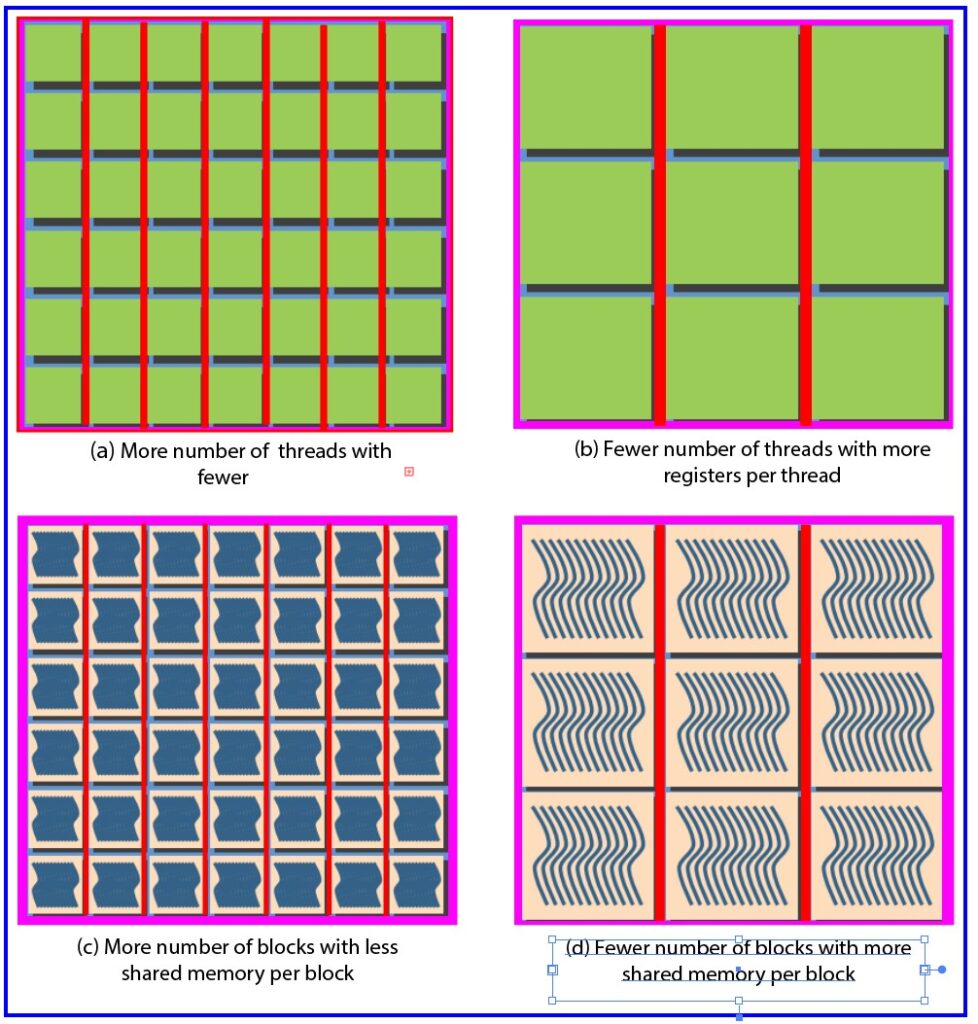
Fig. Pictorial representation of resources partitioning.
Latency Hiding
Latency hiding is a critical aspect of GPU programming, primarily in the context of parallel computing using NVIDIA’s CUDA C++ framework. It refers to the ability to mask or reduce the impact of high-latency operations, such as memory transfers or instruction pipeline stalls, by overlapping them with other useful computation. By doing so, applications can continue to make progress while waiting for these operations to complete, thereby improving overall throughput and minimizing the time wasted due to latency.
In CUDA programming, latency hiding is particularly important because GPUs are designed to handle massive parallelism. However, they often consist of thousands of lightweight processing cores, which means that they can execute a large number of threads simultaneously. To harness the full power of a GPU, developers must ensure that these threads remain active and productive.
The Significance of Latency Hiding
Understanding why latency hiding is crucial in CUDA C++ development is the first step toward effective GPU optimization. Latency in computing refers to the delay or time gap between the initiation of a request and the receipt of the corresponding response. This delay can be caused by various factors, including memory access times, data transfer between the CPU and GPU, or pipeline stalls due to dependencies.
The significance of latency hiding can be summarized as follows:
Improved Utilization: In a highly parallel environment like a GPU, efficient resource utilization is paramount. When one thread is stalled due to latency (e.g., waiting for data to be fetched from memory), other threads can continue executing. Latency hiding ensures that the GPU cores are actively processing threads, thus improving overall throughput.
Reduced Bottlenecks: By overlapping latency-prone operations with productive computations, developers can alleviate bottlenecks that would otherwise limit the GPU’s performance. This is especially critical when dealing with memory-bound applications.
Real-Time Responsiveness: Latency hiding is vital in applications where real-time responsiveness is required. By minimizing delays, tasks can be completed more quickly, making latency-sensitive applications, such as simulations and image processing, more efficient.
Optimized GPU Performance: To maximize the capabilities of a GPU, it is essential to keep the processing units active. Latency hiding helps in achieving high GPU utilization, which is vital for demanding tasks like deep learning, scientific simulations, and data processing.
Techniques for Latency Hiding
Here are brief descriptions of latency hiding techniques in CUDA GPU.
Asynchronous Execution: This technique involves launching GPU tasks asynchronously, allowing the CPU to initiate tasks and proceed with other computations without waiting for the GPU to finish. It enables overlapping CPU and GPU computations to hide latency effectively.
Overlapping Communication and Computation: Overlapping communication, such as data transfers, with computation is a strategy to minimize latency. By initiating data transfers and GPU computations in parallel, the GPU can process data while the transfer is in progress.
Shared Memory and Register Spilling: Using shared memory to reduce global memory access and spilling registers to slower memory when the kernel uses more registers than available on a multiprocessor. These techniques help minimize latency by optimizing memory access.
Dynamic Parallelism: Dynamic parallelism allows a GPU kernel to launch other kernels, initiating new work while previous work is still in progress. This technique hides latency by enabling additional tasks to run concurrently.
Pipelining: Pipelining divides complex tasks into stages, allowing each stage to begin execution as soon as its inputs are available. This minimizes idle time and ensures a continuous flow of work, reducing latency’s impact.
Kernel Fusion: Kernel fusion involves merging multiple smaller kernels into a single, more substantial kernel. This reduces kernel launch overhead and the time between different kernel executions, thus minimizing latency.
CUDA Memory Model
Introduction
Efficient memory handling is a crucial aspect of all programming languages. In high-performance computing , memory management plays very significant role. Many tasks depend on the speed at which data can be loaded and stored. Having abundant low-latency, high-bandwidth memory can significantly boost performance. However, acquiring large, high-performance memory isn’t always feasible or cost-effective.
In such situations, the memory model becomes crucial. It allows you to fine-tune the balance between latency and bandwidth, customizing data placement according to the hardware memory subsystem. CUDA’s memory model accomplishes this seamlessly by harmonizing host and device memory systems, granting you full access to the memory hierarchy. This explicit control over data placement optimizes performance without the need for extravagant memory resources.
Principle Of Locality
Applications do not access arbitrary data or execute arbitrary code at any point in time. Instead, applications often follow the principle of locality, which suggests that they access a relatively small and localized portion of their address space at any point in time. This principle is categorized into two primary types of locality:
Spatial Locality: This principle indicates that if a program accesses a particular memory location, it’s likely to access nearby memory locations soon afterward. This is a result of data structures or loops that group related data together in memory. When threads cooperate and access adjacent memory, spatial locality is enhanced, resulting in efficient memory access.
Temporal Locality: Temporal locality suggests that if a program accesses a memory location, it’s likely to access the same location in the near future. This is common in loops and recurring operations where the same data is accessed repeatedly. Caches and shared memory are essential in exploiting temporal locality, reducing the need to access slower global memory.
Memory Hierarchy
The memory hierarchy is a fundamental framework that governs how the GPU manages data. This hierarchy relies on two types of memory: one with low latency and limited storage capacity, used for actively processed data, and another with high latency and ample storage capacity, reserved for future tasks. A strong grasp of this hierarchy is essential for unlocking the full computational potential of GPUs.
To boost performance, modern computer systems employ a memory hierarchy concept. This concept encompasses multiple memory levels, each offering different data access speeds. However, quicker access on some levels often comes at the expense of reduced storage space. The reason this hierarchy matters lies in the principle of locality, leading to the incorporation of various memory levels, each with its distinctive attributes, such as access speed, data transfer capabilities, and storage capacity.
The CUDA memory model provides access to various programmable memory types, including registers, shared memory, local memory, constant memory, texture memory, and global memory. The figure below provides a clear visual representation of the hierarchy of these memory spaces, each characterized by its scope, lifespan, and caching behavior.
Every thread within a kernel has its own private local memory, while a thread block has its own shared memory, visible to all threads in that block and persisting for the duration of the block’s execution. Global memory is accessible to all threads, and there are two read-only memory spaces available to all threads: constant and texture memory. Global, constant, and texture memory spaces are each optimized for distinct purposes. Texture memory offers diverse address modes and filtering options for various data layouts, and the contents of global, constant, and texture memory have the same lifespan as the application. Let us discuss each memory types one by one.
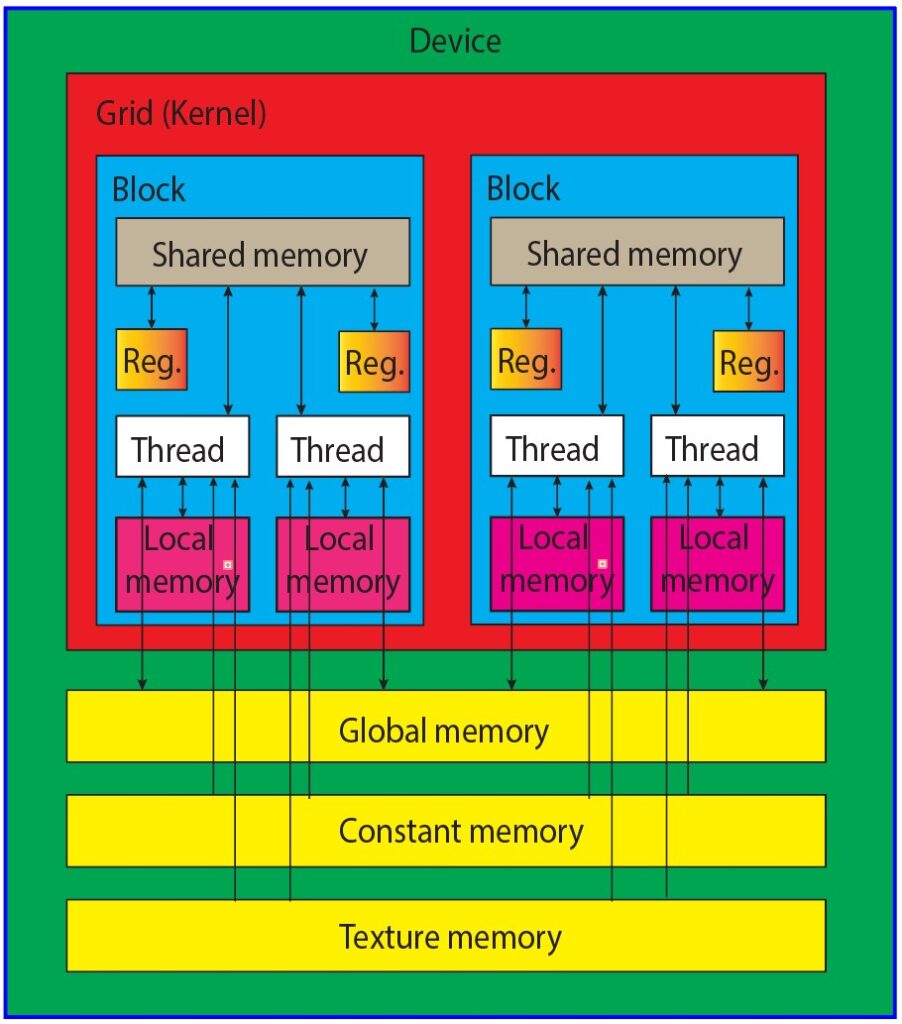
Fig. Cuda memory Model
- Registers: Registers represent the fastest form of memory available on a GPU. Any automatic variable declared within a kernel without additional type qualifiers is typically stored in a register. In certain cases, arrays declared in a kernel can also be allocated to registers, but this only occurs when the array indices are constant and can be determined at compile time. These register variables are private to each individual thread and are primarily used to store frequently accessed thread-private data within a kernel. It’s important to note that the lifetime of register variables is limited to the duration of the kernel’s execution. Once a kernel completes its execution, any register variable becomes inaccessible. Registers are a finite and valuable resource allocated among active warps in a Streaming Multiprocessor (SM).
- Local memory: Variables within a kernel that meet the criteria for registers but exceed the available register capacity are redirected to local memory. Variables that the compiler is inclined to allocate to local memory are local arrays accessed using indices with values that cannot be ascertained at compile-time, and large local structures or arrays that would overconsume the allocated register space, and any variable surpassing the kernel’s register limit. It is essential to recognize that the term “local memory” can be somewhat misleading. Values spilling into local memory physically reside in the same location as global memory. Accessing local memory involves high latency, low bandwidth, and is subject to the efficiency requirements for memory access patterns described later in this chapter.
- Shared Memory: Shared memory, residing on the GPU’s chip, offers significantly higher bandwidth and reduced latency compared to local or global memory. It functions in a manner akin to the L1 cache in a CPU but remains programmable. Each Streaming Multiprocessor (SM) possesses a finite portion of shared memory, allocated among different thread blocks. Consequently, it is crucial not to excessively consume shared memory, as doing so inadvertently restricts the number of active warps. Shared memory is declared within the scope of a kernel function but shares its lifespan with a specific thread block. Once a thread block completes its execution, the shared memory it was assigned is relinquished and reallocated to other thread blocks. This shared memory plays a fundamental role in facilitating inter-thread communication, enabling threads within a block to collaborate by exchanging data stored within it. The shared memory can be declared the __shared__ keyword followed by the data type and variable name. For example:
__shared__ int sharedData[256];
- Constant Memory: Constant memory is designed for storing read-only data, primarily constants. This can include mathematical constants, lookup tables, or other values that don’t change during the kernel’s operation. When data is first accessed from constant memory, it’s cached, making subsequent reads significantly faster. This is particularly beneficial when multiple threads need to access the same constant data, as it reduces memory access latency. Constant memory has a limited capacity, so it’s essential to use it judiciously. Attempting to store large amounts of data in constant memory can lead to resource limitations. The constant memory is declared using the __constant__ keyword. For example:
__constant__ float myConstantValue;
- Texture Memory: Texture memory is designed to optimize texture access for GPU applications, especially those related to graphics, image processing, and computer vision. It provides a convenient and efficient way to store and retrieve data, such as textures, that are frequently accessed during GPU computation. Texture memory is cached, which means that data is temporarily stored in a high-speed cache. Texture memory is primarily intended for storing read-only data, such as textures used in graphics applications. While you can read from texture memory, it’s not designed for direct writes or modifications.
- Global Memory: Global memory is one of the primary memory spaces in a GPU, typically associated with the GPU’s DRAM (Dynamic Random-Access Memory). It is the largest memory space available in the GPU and is accessible to all threads running on the GPU. Global memory offers a substantial storage capacity, making it suitable for storing large datasets and variables. It is especially valuable when dealing with massive data arrays. Global memory is relatively slow when compared to other memory types. This is because it is physically located off-chip, which means that accessing data from global memory takes more time compared to on-chip memory like shared memory or registers. Data stored in global memory is accessible by any thread within any thread block. This allows them to be accessible from any function or kernel within your CUDA program. You can declare global memory statically or dynamically, depending on your program’s requirements.
The key characteristics of the different memory types are also outlined in the Table below.
| Memory Type | On/Off Chip | Access | Scope | Lifetime | Cached |
|---|---|---|---|---|---|
| Registers | On-Chip | R/W | 1 thread | Thread | No |
| Local Memory | Off-Chip | R/W | 1 thread | Thread | No |
| Shared Memory | On-Chip | R/W | All threads in block | Block | No |
| Global Memory | Off-Chip | R/W | All threads + host | Host allocation | No |
| Constant Memory | Off-Chip | R | All threads + host | Host allocation | Yes |
| Texture Memory | Off-Chip | R | All threads + host | Host allocation | Yes |
Global Memory
Global memory is a fundamental component of memory management in CUDA programming. It plays a central role in enabling the parallel processing capabilities of GPUs (Graphics Processing Units) and is critical for harnessing the full computational power of these devices. In this detailed explanation, we will explore global memory, covering its characteristics, allocation, data transfer, synchronization, coalescence, and optimization.
Characteristics of Global Memory
Global memory in CUDA represents a large, off-chip memory space that is accessible by all threads in a GPU. It is the primary means of data sharing and communication between threads, and it exhibits several key characteristics:
-
Capacity: Global memory is the largest memory space in the GPU. It offers a substantial storage capacity, making it suitable for storing large datasets and variables required by parallel algorithms.
-
Latency: While global memory provides ample storage, it is relatively slow when compared to other memory types in the GPU memory hierarchy. This latency stems from the physical off-chip location of global memory.
-
Accessibility: Global memory is a universal memory space that can be accessed by any thread within any block. This accessibility makes it a primary choice for storing and sharing data across threads.
-
Persistence: Data stored in global memory persists across multiple kernel launches. It maintains its state throughout the entire program execution on the GPU, allowing data to be shared and used by different stages of the program.
Allocation and Deallocation:
Allocating memory in global memory is the first step in utilizing this memory space effectively. Memory allocation in CUDA is achieved through the cudaMalloc() function, which reserves a specified amount of global memory to store data. To allocate global memory, you need to provide the size of the memory block you wish to allocate. The function returns a pointer to the allocated memory, which can be used to access and manipulate the data stored in global memory. Here’s an example of how to allocate memory in global memory:
int* deviceData; // Pointer to device (GPU) memory
// Allocate memory on the GPU
cudaMalloc((void**)&deviceData, sizeof(int) * dataSize);
// Check for successful memory allocation
if (deviceData == nullptr) {
// Handle memory allocation failure
}
In this example, cudaMalloc() is used to allocate an array of integers on the GPU. The size of the allocation is determined by sizeof(int) * dataSize, where dataSize represents the number of integers to be stored. It is also important to check for the success of memory allocation, as the allocation may fail if there is insufficient available global memory. A failure to allocate memory should be handled gracefully in your CUDA application.
Deallocating global memory is equally important to prevent memory leaks. The cudaFree() function is used to release the allocated memory when it is no longer needed.
cudaFree(deviceData); // Deallocate global memory
By deallocating memory, you ensure that resources are freed up for other parts of your program.
Data Transfer
Efficient data transfer between the CPU (host) and the GPU (device) is crucial for CUDA applications. Data often needs to be moved between these two entities for processing or to share results. CUDA provides functions like cudaMemcpy() for data transfer between host and device memory. There are several memory copy directions in CUDA:
- cudaMemcpyHostToHost: Data transfer from host to host.
- cudaMemcpyHostToDevice: Data transfer from host to device.
- cudaMemcpyDeviceToHost: Data transfer from device to host.
- cudaMemcpyDeviceToDevice: Data transfer from device to device.
Here’s an example of how to use cudaMemcpy() to transfer data from the host to the device:
int* hostArray; // Pointer to host (CPU) memory
int* deviceArray; // Pointer to device (GPU) memory
// Allocate memory on the CPU and the GPU
hostArray = (int*)malloc(sizeof(int) * arraySize);
cudaMalloc((void**)&deviceArray, sizeof(int) * arraySize);
// Copy data from the host to the device
cudaMemcpy(deviceArray, hostArray, sizeof(int) * arraySize, cudaMemcpyHostToDevice);
In this code snippet, data stored in hostArray on the CPU is copied to deviceArray on the GPU using cudaMemcpy(). The function handles the data transfer efficiently, ensuring that the data arrives correctly on the GPU. The direction of data transfer is specified as cudaMemcpyHostToDevice.
Efficient data transfer is vital for maintaining the overall performance of CUDA applications, particularly when handling large datasets. It’s important to manage data transfers carefully to minimize overhead and latency.
Synchronization
Synchronization in CUDA is essential for ensuring that data transfers and kernel executions are coordinated correctly. Data transfers between the host and the device should be synchronized to avoid accessing data that has not yet arrived or has not yet been transferred. Additionally, synchronization between kernels is crucial to guarantee that one kernel does not start executing before another has completed.
You can use CUDA events and synchronization primitives to coordinate data transfers and kernel execution. CUDA events, such as cudaEvent_t, allow you to record points in time during the execution of your CUDA code. You can use these events to measure time or to synchronize actions. Here’s an example of how to use events for synchronization:
cudaEvent_t start, stop;
float elapsedTime;
// Create events
cudaEventCreate(&start);
cudaEventCreate(&stop);
// Record the start event
cudaEventRecord(start);
// Launch a kernel
myKernel<<<blocksPerGrid, threadsPerBlock>>>(deviceData);
// Record the stop event
cudaEventRecord(stop);
// Synchronize and calculate the elapsed time
cudaEventSynchronize(stop);
cudaEventElapsedTime(&elapsedTime, start, stop);
// Cleanup events
cudaEventDestroy(start);
cudaEventDestroy(stop);
In this example, two events (start and stop) are created and used to measure the elapsed time between recording the start and stop events. Synchronization is achieved using cudaEventSynchronize(). This ensures that the time measurement is accurate and that the kernel executes correctly in relation to other events.
Proper synchronization is particularly important when launching multiple kernels in sequence, as it helps maintain the correct order of execution and data availability.
Coalesced Memory Access
Efficient memory access patterns are crucial for optimizing GPU performance. Coalesced memory access is a memory access pattern that minimizes memory access conflicts and maximizes memory throughput. It is achieved by ensuring that threads in a warp (a group of threads executed together) access contiguous memory locations in global memory.
Coalesced memory access provides efficient data retrieval and reduces memory access overhead. When memory accesses are coalesced, threads in a warp can access a larger chunk of data in a single transaction, reducing the number of transactions required to retrieve data. This leads to improved memory bandwidth and overall performance.
To achieve coalesced memory access, it’s essential to organize data structures and access patterns to minimize conflicts. Threads should be designed to access adjacent memory locations, ensuring that consecutive threads in a warp access consecutive data elements.
__global__ void coalescedAccess(int* data) {
int tid = threadIdx.x + blockIdx.x * blockDim.x;
// Ensure coalesced memory access by accessing consecutive elements
int value = data[tid];
}
In this code, each thread in the kernel accesses consecutive elements in the global memory array, leading to coalesced memory access and improved memory throughput.

Dr. Partha Majumder is a distinguished researcher specializing in deep learning, artificial intelligence, and AI-driven groundwater modeling. With a prolific track record, his work has been featured in numerous prestigious international journals and conferences. Detailed information about his research can be found on his ResearchGate profile. In addition to his academic achievements, Dr. Majumder is the founder of Paravision Lab, a pioneering startup at the forefront of AI innovation.



I don’t think the title of your article matches the content lol. Just kidding, mainly because I had some doubts after reading the article.
Can you be more specific about the content of your article? After reading it, I still have some doubts. Hope you can help me.